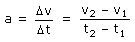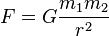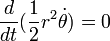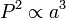Materi Fisika Kelas XI Semester 1

FISIKA

1. PERSAMAAN GERAK

Koordinat Polar Titik P dengan koordinat polar (r, q) berarti berada diposisi: - q derajat dari sumbu-x (sb. polar) (q diukur berlawanan arah jarum-jam) - berjarak sejauh r dari titik asal kutub O. Perhatian: jika r <> r: koordinat radial q: koordinat sudut Setiap titik mempunyai lebih dari satu representasi dalam koordinat polar (r, q) = (- r, q + np ), untuk n bil. bulat ganjil = ( r, q + np ) , untuk n bil. bulat genap Persamaan dalam Koordinat Polar Pers. polar dari lingkaran berjari-jari a: r = a Untuk lingkaran berjari a, - berpusat di (0,a): r = 2a sin q - berpusat di (a,0): r = 2a cos q r = 2 sin q r = 2 cos qVektor posisi, kecepatan dan percepatan. V adalah kecepatan benda yang merupakan turunan pertama dari posisi. Jadi Vx adalah turunan pertama dari X dan Vy adalah turunan pertama dari Y. Silakan kamu turunkan (diferensialkan) persamaan tersebut... Vox adalah Vx saat t = 0, dan Voy adalah Vy saat t = 0. Vo adalah penjumlahan (secara vektor) dari Vox dan Voy. Ax adalah turunan kedua dari X, dan Ay adalah turunan kedua dari Y. Coba kamu turunkan sendiri.... Aox adalah Ax saat t = 0, dan Aoy adalah Ay saat t = 0.Mengubah persamaan posisi menjadi percepatanA :Jika posisi benda dinyatakan dalam persamaan dengan variable waktu, maka persamaan posisi tersebut kita turunkan (diferensialkan) menjadi persamaan kecepatan. misal, x = 2t^2 - 2t maka kecepatannya adalah turunan pertama dari x; v = dx/dt = 4t - 2 untuk mengubah menjadi percepatan, maka kecepatan tersebut kita turunkan sekali lagi; a = dv/dt = 4

# Gerak Lurus Beraturan (GLB) #

Gerak lurus beraturan (GLB) adalah gerak benda dalam lintasan garis lurus dengan kecepatan tetap. Untuk lebih memahaminya, amati grafik berikut :

Grafik di atas menyatakan hubungan antara kecepatan (v) dan waktu tempuh (t) suatu benda yang bergerak lurus. Berdasarkan grafik tersebut cobalah tentukan berapa besar kecepatan benda pada saat t = 0 s, t = 1 s, t = 2 s, t = 3 s?
Tampak dari grafik pada gambar 6,
kecepatan benda sama dari waktu ke waktu yakni 5 m/s.
Semua benda yang bergerak lurus beraturan akan memiliki grafik v - t yang bentuknya seperti gambar 6 itu. Sekarang,hitung berapa jarak yang ditempuh oleh benda dalam waktu 3 s?
dapat dihitung jarak yang ditempuh oleh benda dengan cara menghitung luas daerah di bawah kurva bila diketahui grafik (v-t) :

Jarak yang ditempuh = luas daerah yang diarsir pada grafik v - t.
Cara menghitung jarak pada GLB.Tentu saja satuan jarak adalah satuan panjang, bukan satuan luas. Berdasarkan gambar di atas, jarak yang ditempuh benda = 15 m.

Cara lain menghitung jarak tempuh adalah dengan menggunakan persamaan GLB.

kecepatan pada GLB dirumuskan:

Ket : v = kecepatan (m/s) t = waktu tempuh (s) s = Jarak (m)

Dari gambar di atas ,
v = 5 m/s,sedangkan t = 3 s, sehingga jarak s = v . ts = 5 x 3 = 15 m
Persamaan GLB di atas, berlaku bila gerak benda memenuhi grafik seperti pada gambar.

Pada grafik tersebut terlihat bahwa pada saat t = 0 s, maka v = 0.

Artinya, pada mulanya benda diam, baru kemudian bergerak dengan kecepatan 5 m/s. Padahal dapat saja terjadi bahwa saat awal kita amati benda sudah dalam keadaan bergerak, sehingga benda telah memiliki posisi awal so. Untuk keadaan ini, maka persamaan GLB sedikit mengalami perubahan menjadi,
s = so + v.
Persamaan GLB untuk benda yang sudah bergerak sejak awal pengamatan.
Dengan so menyatakan posisi awal benda dalam satuan meter.
Di samping grafik v - t di atas, pada gerak lurus terdapat juga grafik s-t, yakni grafik yang menyatakan hubungan antara jarak tempuh (s) dan waktu tempuh (t) seperti pada gambar di bawah.
Pada saat t = 0 s, jarak yang ditempuh oleh benda s = 0, pada saat t = 1 s, jarak yang ditempuh oleh benda s = 2 m, pada saat t = 2 s, jarak s = 4 m, pada saat t = 3 s, jarak s = 6 s dan seterusnya. Berdasarkan hal ini dapat kita simpulkan bahwa benda yang diwakili oleh grafik s - t pada gambar 9 di atas, bergerak dengan kecepatan tetap 2 m/s (Ingat, kecepatan adalah jarak dibagi waktu).

Berdasarkan gambar, kita dapat meramalkan jarak yang ditempuh benda dalam waktu tertentu di luar waktu yang tertera pada grafik.

contoh :

Gerak sebuah benda yang melakukan GLB diwakili oleh grafik s - t di bawah. Berdasarkan grafik tersebut, hitunglah jarak yang ditempuh oleh benda itu dalam waktu:
a. 3 s
b. 10 s

Jawab :

Diketahui:
so = 2 m
v = 4 m/s

Ditanya:
a. Jarak yang ditempuh benda pada saat t = 3 s.
b. Jarak yang ditempuh benda pada saat t = 10 s.

Jawab:

a.

s (t) s (3s)

= so + v.t = 2 + 4 x 3 = 14 m

b.

s (t) s (10s)

= so + v.t = 2 + 4 x 10 = 42 m

# GERAK LURUS BERUBAH BERATURAN (GLBB) #

Gerak lurus berubah beraturan (GLBB) adalah gerak benda dalam lintasan garis lurus dengan percepatan tetap. Jadi, ciri utama GLBB adalah bahwa dari waktu ke waktu kecepatan benda berubah, semakin lama semakin cepat. Dengan kata lain gerak benda dipercepat. Namun demikian, GLBB juga dapat berarti bahwa dari waktu ke waktu kecepatan benda berubah, semakin lambat hingga akhirnya berhenti. Dalam hal ini benda mengalami perlambatan tetap. Dalam modul ini, kita tidak menggunakan istilah perlambatan untuk gerak benda diperlambat. Kita tetap saja menamakannya percepatan, hanya saja nilainya negatif. Jadi perlambatan sama dengan percepatan negatif.

Contoh sehari-hari GLBB adalah peristiwa jatuh bebas. Benda jatuh dari ketinggian tertentu di atas. Semakin lama benda bergerak semakin cepat.

perhatikanlah gambar di bawah yang menyatakan hubungan antara kecepatan (v) dan waktu (t) sebuah benda yang bergerak lurus berubah beraturan dipercepat.

a. Besar percepatan benda

dalam hal ini,
v1 = vo
v2 = vt
t1 = 0
t2 = t

sehingga ,

atau a.t = vt - vo kita dapatkan :


persamaan kecepatan GLBB :
ket : vo = kecepatan awal (m/s)
vt = kecepatan akhir (m/s)
a = percepatan ()
t = selang waktu (s) kecepatan benda berubah dari vo menjadi vt sehingga kecepatan rata-rata benda dapat dituliskan:













b. Kecepatan rata-rata :

ket : s = Jarak yang ditempuh a = percepatan ( ) vo = lecepatan awal (m/s) t = selang waktu (s) contoh :

	Benda yang semula diam didorong sehingga bergerak dengan percepatan tetap 3 . Berapakah besar kecepatan benda itu setelah bergerak 5 s? Penyelesaian: Awalnya benda diam, jadi vo = 0 a = 3 t = 5 s Kecepatan benda setelah 5 s:
	vt	= vo + a.t = 0 + 3 . 5 = 15 m/s

# GERAK MELINGKAR BERUBAH BERATURAN #
Adalah gerak suatu benda dengan bentuk lintasan melingkar dan besar percepatan sudut/anguler (α) konstan.

Jika perecepatan anguler benda searah dengan perubahan kecepatan anguler maka perputaran benda semakin cepat, dan dikatakan GMBB dipercepat. Sebaliknya jika percepatan anguler berlawanan arah dengan perubahan kecepatan anguler benda akan semakin lambat, dan dikatakan GMBB diperlambat.

1. Percepatan Anguler (α)

Sebuah benda bergerak melingkar dengan laju anguler berubah beraturan memiliki perubahan kecepatan angulernya adalah :

Δω = ω₂ – ω₁

Dan perubahan waktu kecepatan anguler adalah Δt, maka di dapatkan :

∆ω = perubahan kecepatan sudut (rad/s)
∆t = selang waktu (s)
α = percepatan sudut/anguler (rads^-2)

Sama halnya dengan Gerak Lurus Berubah Beraturan (GLBB), pada GMBB berlaku juga :

- Mencari kecepatan sudut akhir (ω_t) :

ω_t = ω₀ ± α.t

- Mencari posisi sudut / besar sudut (θ) yang ditempuh:

θ= ω₀ t ± α.t²

x = R. θ

Dapat diperoleh juga :

ωt² = ω₀² ± 2 α.θ

dimana :

ωt = kecepatan sudut/anguler keadaan akhir(rad/s)
ω0 = kecepatan sudut/anguler keadaan awal (rad/s)
θ = besar sudut yang ditempuh (radian, putaran)
1 rpm = 1 putaran permenit
1 putaran = 360° = 2p rad.
x = perpindahan linier (m)
t = waktu yang diperlukan (s)
R = jari-jari lintasan (m)

# GERAK MELINGKAR BERATURAN #

Adalah partikel yang bergerak melingkar dengan laju konstan, arah vektor kecepatan berubah terus menerus, tetapi besarnya tidak.

Dalam gerak lurus anda mengenal besaran perpindahan (linear) dan kecepatan (linear), keduanya termasuk besaran vektor. Dalam gerak melingkar anda akan mengenal juga besaran yang mirip dengan itu, yaitu perpindahan sudut dan kecepatan sudut, keduanya juga termasuk besaran vektor.

Besaran fisis pada GMB

a. Besaran Sudut (Ø)

Besar sudut Ø dinyatakan dalam derajat tetapi pada gerak melingkar beraturan ini dinyatakan dalam radian. Satu radian (rad) adalah sudut dimana panjang busur lingkaran sama dengan jari-jari lingkaran tersebut (r). Jika s = r, Ø bernilai 1 rad.

Secara umum besaran sudut Ø dituliskan :

Ø = s / r

dimana s = 2∏ r , sehingga Ø = 2∏ rad

b. Kecepatan dan kelajuan Sudut (ω)

Pada gerak melingkar, besaran yang menyatakan seberapa jauh benda berpindah (s) dalam selang waktu tertentu (t) disebut kecepatan anguler atau kecepatan sudut (ω). Kecepatan sudut ini terbagi atas kecepatan sudut rata-rata dan kecepatan sudut sesaat.

Kecepatan sudut rata-rata dituliskan sebagai : ω = ΔØ / Δt

Kecepatan sudut sesaat dinyatakan sebagai ω = lim ΔØ / Δt

Satuan kecepatan sudut adalah rad/s. Selain satuan ini, satuan kecepatan sudut dapat pula ditulis dalam rpm (rotation per minutes) dimana 1 rpm = 2Π rad/menit = Π/30 rad/s.

Sedangkan nilai atau besarnya kecepatan sudut disebut kelajuan sudut.

c. Periode (T)

Waktu yang dibutuhkan oleh suatu benda untuk bergerak satu putaran disebut periode (T). Waktu yang dibutuhkan untuk menempuh satu putaran dinyatakan oleh :

T = perpindahan sudut / kecepatan sudut

T = 2Π / ω dimana 2Π = perpindahan sudut (anguler) untuk satu putaran.

Jika jumlah putaran benda dalam satu sekon dinyatakan sebagai frekuensi (f) maka diperoleh hubungan :

T = 1 / f dimana f = frekuensi dengan satuan 1/s atau Hertz (Hz).

d. Kecepatan dan kelajuan linear (v)

Kecepatan linear didefinisikan sebagai hasil bagi panjang lintasan linear yang ditempuh dengan selang waktu tempuhnya. Panjang lintasan dalam gerak melingkar yaitu keliling lingkaran 2Π.r

Jika selang waktu yang diperlukan untuk menempuh satu putaran adalah 1 periode (T), maka :

Kecepatan linear dirumuskan : v = 2Π.r / T atau v = ω.r

Kecepatan linear ( v) memiliki satuan m/s, r = jari-jari lintasan, dengan satuan meter dan ω = kecepatan sudut dalam satuan rad/s

e. Percepatan Sentripetal

Pada saat anda mempelajari gerak lurus beraturan sudah mengetahui bahwa percepatan benda sama dengan nol. Benarkah kalau kita juga mengatakan percepatan benda dalam gerak melingkar beraturan sama dengan nol? Dari gambar di atas diketahui bahwa arah kecepatan linear pada gerak melingkar beraturan selalu menyinggung lingkaran. Karena itu, kecepatan linear disebut juga kecepatan tangensial.

Sekarang kita akan mempelajari apakah vektor percepatan pada benda yang bergerak melingkar beraturan nol atau tidak.Dari gambar di atas tampak bahwa vektor kecepatan linear memiliki besar sama tetapi arah berbeda-beda. Oleh karena itu kecepatan linear selalu berubah sehingga harus ada percepatan. Dari gambar di atas tampak bahwa arah percepatan selalu mengarah ke pusat lingkaran dan selalu tegak lurus dengan kecepatan linearnya. Percepatan yang selalu tegak lurus terhadap kecepatan linearnya dan mengarah ke pusat lingkaran ini disebut percepatan sentripetal.

Percepatan sentripetal pada gerak melingkar beraturan dirumuskan :

Contoh Soal :

Sebuah roda dengan jari-jari 20 cm, berputar pada sumbunya dengan kelajuan 6.000/Π rpm. Tentukan: (a). kelajuan sudut, frekuensi, dan periodenya, (b). kelajuan linear sebuah titik atau dop pada roda dan panjang lintasan titik yang ditempuh selama 10 s. (c) jumlah putaran dalam 10 s.

Pembahasan :

1. diketahui : r = 20 cm = 0,2 m ; ω = 6.000/Π rpm = 100/Π rps = 200 rad/s

dijawab :

(a). Frekuensi f = ω / 2Π = (200 rad/s)/2Π = 100/Π Hz

(b). Kelajuan linear pada titik luar

v = ω . r = (200 rad/s). (0,2 m) = 40 m/s

(c) Jumlah putaran selama 10 s. Sudut yang ditempuh selama 10 s adalah Ø = ω . t = 2.000 rad

1 putaran = 2Π rad sehingga jumlah putaran (n) adalah n = 2.000 rad/2Π =(1000/Π ) putaran.

2. Sebuah benda bergerak melingkar beraturan dengan jari-jari lintasan 70 cm. Dalam waktu 20 s, benda tersebut melakukan putaran sebanyak 40 kali. (a). tentukan periode dan frekuensi putaran. (b) berapa laju linear benda tersebut? (c). hibunglah kecepatan sudut benda tersebut.

# GERAK PARABOLA #

Gerak parabola panduan dari GLB pada sumbu x dengan GLB pada sumbu y.

Kecepatan awal (v_o) gerak benda diwakili oleh v_0x dan v_0y. v_0x merupakan kecepatan awal pada sumbu x, sedangkan v_0y merupakan kecepatan awal pada sumbu y. v_y merupakan komponen kecepatan pada sumbu y dan v_x merupakan komponen kecepatan pada sumbu x. Pada titik tertinggi lintasan gerak benda, kecepatan pada arah vertikal (v_y) sama dengan nol.

Persamaan untuk menghitung posisi dan kecepatan resultan dapat dirumuskan sebagai berikut.

2. GAYA

Gaya adalah tarikan atau dorongan yang diberikan kepada suatu benda.

* Macam-macam gaya :

a. Gaya Normal

Ketika balok jatuh telah sampai kelantai gaya gravitasi tetap bekerja walaupun benda sudah berhenti. Sesuai Hukum III Newton , gaya aksi (Gaya Berat) yang dikerjakan benda pada lantai akan menimbulkan gaya reaksi dari lantai pada benda gaya ini di sebut Gaya Normal.
Arah gaya normal selalu tegak lurus dengan permukaan sentuh.

Ada beberapa gaya normal pada benda berdasarkan posisi benda:

b. Gaya Gesekan

Gaya gesekan adalah gaya yang ditimbulkan ketika dua permukaan benda saling bersentuhan. Arah Gaya gesekan selalu berlawanan dengan arah gerak benda. Ada dua jenis gaya gesekan, yakni :

• Gaya gesekan statis

Gaya gesekan statis adalah gaya gesekan yang menyebabkan benda tidak dapat bergerak (statis ). Nilai gaya gesekan statis maksimum pada benda artinya jika kita ingin mendorong benda sampai dapat bergerak besarnya gaya yang dikerjakan harus lebih besar daripada gaya gesek statis maksimum.
Besarnya gaya ini:

dimana
µs = koefisien gesek statis
N = Besarnya gaya normal pada benda

Mengapa anak tersebut tidak mampu membuat lemari brankas bergerak..?

Hal itu terjadi karena gaya yang di berikan anak itu masih lebih kecil dari pada gaya gesek statis maksimum lemari brankas.

Apa yang terjadi bila anak itu mendorong dengan di bantu kakaknya yang lebih dewasa?

Ternyata brankas itu dapat bergerak walaupun lajunya lambat.

Kelajuan lambat ini di karenakan gaya gesek statis yang bekerja pada lemari brankas.

• Gaya gesekan kinetis

Gaya gesek kinetis adalah gaya gesek yang terjadi saat benda bergerak.gaya gesek kinetis menghambat laju benda, arah gaya gesek kinetic berlawanan dengan arah gerak benda. Besarnya gaya gesek kinetis adalah:

Dimana:
µk = koefisien gesek kinetic
N = Gaya normal benda, Newton

c. Gaya Sentripetal

Gaya Sentripetal adalah gaya yang di miliki benda saat benda bergerak dalam lintasan berbentuk lingkaran, dengan gaya sentripetal benda dapat bertahan pada lintasannya.

Perhatikan gerak benda di bawah ini!

Gaya sentripetal pada tali menyebabkan benda tetap dalam lintasan melingkar.

d. Gaya Gravitasi

Gaya Gravitasi

Gravitasi adalah gaya tarik-menarik yang terjadi antara semua partikel yang mempunyai massa di alam semesta. Fisika modern mendeskripsikan gravitasi menggunakan Teori Relativitas Umum dari Einstein, namun hukum gravitasi universal Newton yang lebih sederhana merupakan hampiran yang cukup akurat dalam kebanyakan kasus.

Sebagai contoh, Bumi yang memiliki massa yang sangat besar menghasilkan gaya gravitasi yang sangat besar untuk menarik benda-benda disekitarnya, termasuk makhluk hidup, dan benda benda yang ada di bumi. Gaya gravitasi ini juga menarik benda-benda yang ada diluar angkasa, seperti bulan, meteor, dan benda angkasa laiinnya, termasuk satelite buatan manusia.

Beberapa teori yang belum dapat dibuktikan menyebutkan bahwa gaya gravitasi timbul karena adanya partikel gravitron dalam setiap atom.

Hukum Gravitasi Universal Newton

Hukum gravitasi universal Newton dirumuskan sebagai berikut:

Setiap massa titik menarik semua massa titik lainnya dengan gaya segaris dengan garis yang menghubungkan kedua titik. Besar gaya tersebut berbanding lurus dengan perkalian kedua massa tersebut dan berbanding terbalik dengan kuadrat jarak antara kedua massa titik tersebut.

F adalah besar dari gaya gravitasi antara kedua massa titik tersebut

G adalah konstanta gravitasi

m₁ adalah besar massa titik pertama

m₂ adalah besar massa titik kedua

r adalah jarak antara kedua massa titik

Dalam sistem Internasional, F diukur dalam newton (N), m₁ dan m₂ dalam kilograms (kg), r dalam meter (m), dsn konstanta G kira-kira sama dengan 6,67 × 10⁻¹¹ N m² kg⁻².

Dari persamaan ini dapat diturunkan persamaan untuk menghitung Berat. Berat suatu benda adalah hasil kali massa benda tersebut dengan percepatan gravitasi bumi. Persamaan tersebut dapat dituliskan sebagai berikut: W = mg. W adalah gaya berat benda tersebut, m adalah massa dan g adalah percepatan gravitasi. Percepatan gravitasi ini berbeda-beda dari satu tempat ke tempat lain.

Hukum Newton tentang Gaya

Hukum I Newton (Hukum Kelembaman)

Jika resultan gaya yang berkerja pada benda sama dengan nol maka benda yang sedang diam akan tetap diam dan benda bergerak lurus beraturan akan tetap bergerak lurus beraturan

Hukum II Newton

Percepatan suatu benda berbanding lurus dengan gaya yang berkerja pada benda tersebut dan berbanding terbalik dengan massa benda tersebut.

dari gerak balok dapat kita ketahui percepatan system di pengaruhi massa balok.

Contoh soal:

Berapakah gaya yang di butuhkan untuk mempercepat gerak sebuah motor yang bermassa 500 kg pada percepatan 6 m/s²?
Jawab :
F = m.a = 500 . 6 = 3000 N

Hukum III Newton (Hukum aksi dan reaksi)

Bila benda A mengerjakan gaya pada benda B maka benda B akan mengerjakan gaya pada benda A sama besar dengan arah yang berlawanan.

Introduksi Tiga Hukum Kepler

Secara Umum

Hukum hukum ini menjabarkan gerakan dua badan yang mengorbit satu sama lainnya. Masa dari kedua badan ini bisa hampir sama, sebagai contoh Charon—Pluto (~1:10), proporsi yang kecil, sebagain contol. Bulan—Bumi(~1:100), atau perbandingan proporsi yang besar, sebagai contoh Merkurius—Matahari (~1:10,000,000).

Dalam semua contoh diatas kedua badan mengorbit mengelilingi satu pusat masa, barycenter, tidak satupun berdiri secara sepenuhnya di atas fokus elips. Namun kedua orbit itu adalah elips dengan satu titik fokus di barycenter. Jika ratio masanya besar, sebagai contoh planet mengelilingi matahari, barycenternya terletak jauh di tengah obyek yang besar, dekat di titik masanya. Di dalam contoh ini, perlu digunakan instrumen presisi canggih untuk mendeteksi pemisahan barycenter dari titik masa benda yang lebih besar. Jadi, hukum Kepler pertama secara akurat menjabarkan orbit sebuah planet mengelilingi matahari.

Karena Kepler menulis hukumnya untuk aplikasi orbit planet dan matahari, dan tidak mengenal generalitas hukumnya, artikel wikini ini hanya akan mendiskusikan hukum diatas sehubingan dengan matahari dan planet-planetnya.

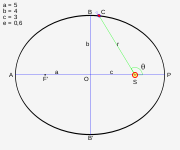
Hukum Pertama

Figure 2: Hukum Kepler pertama menempatkan Matahari di satu titik fokus edaran elips.

"Setiap planet bergerak dengan lintasan elips, matahari berada di salah satu fokusnya."

Pada zaman Kepler, klaim diatas adalah radikal. Kepercayaan yang berlaku (terutama yang berbasis teori epicycle) adalah bahwa orbit harus didasari lingkaran sempurna. Pengamatan ini sangat penting pada saat itu karena mendukung pandangan alam semesta menurut Kopernikus. Ini tidak berarti ia kehilangan relevansi dalam konteks yang lebih modern.

Meski secara teknis elips yang tidak sama dengan lingkaran, tetapi sebagian besar planet planet mengikuti orbit yang bereksentrisitas rendah, jadi secara kasar bisa dibilang mengaproximasi lingkaran. Jadi, kalau ditilik dari observasi jalan edaran planet, tidak jelas kalau orbit sebuah planet adalah elips. Namun, dari bukti perhitungan Kepler, orbit orbit itu adalah elips, yang juga memeperbolehkan benda-benda angkasa yang jauh dari matahari untuk memiliki orbit elips. Benda-benda angkasa ini tentunya sudah banyak dicatat oleh ahli astronomi, seperti komet dan asteroid. Sebagai contoh Pluto, yang diobservasi pada akhir tahun 1930, terutama terlambat diketemukan karena bentuk orbitnya yang sangat elipse dan kecil ukurannya.

Hukum Kedua

Figure 3: Illustrasi hukum Kepler kedua. Bahwa Planet bergerak lebih cepat didekat matahari dan lambat dijarak yang jauh. Sehingga jumlah area adalah sama pada jangka waktu tertentu.

"Luas daerah yang disapu pada selang waktu yang sama akan selalu sama."

Secara matematis:

dimana 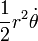adalah "areal velocity".

Hukum Ketiga

Planet yang terletak jauh dari matahari memiliki perioda orbit yang lebih panjang dari planet yang dekat letaknya. Hukum Kepelr ketiga menjabarkan hal tersebut secara kuantitativ.

"Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari matahari."

Secara matematis:

dimana P adalah period orbit planet dan a adalah axis semimajor orbitnya.

Konstant proporsionalitasnya adalah semua sama untuk planet yang mengedar matahari.

e. Gaya Pegas

Bila suatu benda dikenai sebuah gaya dan kemudian gaya tersebut dihilangkan, maka benda akan kembali ke bentuk semula, berarti benda itu adalah benda elastis. Namun pada umumnya benda bila dikenai gaya tidak dapat kembali ke bentuk semula walaupun gaya yang bekerja sudah hilang. Benda seperti ini disebut benda plastis. Contoh benda elastis adalah karet ataupun pegas. Bila pegas ditarik melebihi batasn tertentu maka benda itu tidak akan elastis lagi. Lalu bagaimanakah hubungan pertambahan panjang dengan gaya tarik?

Karena besarnya gaya pemulih sebanding besarnya pertambahan panjang, maka dapat dirumuskan bahwa:


dengan,
k = konstanta pegas
Fp = Gaya Pemulih (N)
x = Perpanjangan Pegas (m)
Persamaan inilah yang disebut dengan Hukum Hooke. Tanda negatif (-) dalam persamaan menunjukkan berarti gaya pemulih berlawanan arah dengan arah perpanjangan.

3. Elastisitas dan Hukum Hooke

Bila suatu benda dikenai sebuah gaya dan kemudian gaya tersebut dihilangkan, maka benda akan kembali ke bentuk semula, berarti benda itu adalah benda elastis. Namun pada umumnya benda bila dikenai gaya tidak dapat kembali ke bentuk semula walaupun gaya yang bekerja sudah hilang. Benda seperti ini disebut benda plastis. Contoh benda elastis adalah karet ataupun pegas. Bila pegas ditarik melebihi batasn tertentu maka benda itu tidak akan elastis lagi. Lalu bagaimanakah hubungan pertambahan panjang dengan gaya tarik?

1. Karena besarnya gaya pemulih sebanding besarnya pertambahan panjang, maka dapat dirumuskan bahwa:
   

   
   
   dengan,
   k = konstanta pegas
   F_p = Gaya Pemulih (N)
   x = Perpanjangan Pegas (m) Persamaan inilah yang disebut dengan Hukum Hooke. Tanda negatif (-) dalam persamaan menunjukkan berarti gaya pemulih berlawanan arah dengan arah perpanjangan.
2. Modulus Elastisitas

   Yang dimaksud dengan Mosdulus Elastisitas adalah perbandingan antara tegangan dan regangan. Modulus ini dapat disebut dengan sebutan Modulus Young.

   1. Tegangan (Stress)
      Tegangan adalah gaya per satuan luas penampang. Satuan tegangan adalah N/m² Secara matematis dapat dituliskan:
      
   2. Regangan (Strain)
      Regangan adalah perbandingan antara pertambahan panjang suatu batang terhadap panjang awal mulanya bila batang itu diberi gaya. Secara matematis dapat dituliskan:
      

   Dari kedua persamaan di atas dan pengertian modulus elastisitas, kita dapat mencari persamaan untuk menghitung besarnya modulus elastisitas, yang tidak lain adalah:
   

   Satuan untuk modulus elastisitas adalah N/m²
3. Gerak Benda di Bawah Pengaruh Gaya Pegas

   Bila suatu benda yang digantungkan pada pegas ditarik sejauh x meter dan kemudian dilepas, maka benda akan bergetar. Percepatan getarnya itu dapat dihitung dengan persamaan:
   

   Dari persamaan di atas, kita mengetahui bahwa besarnya percepatan getar (a) sebanding dan berlawanan arah dengan simpangan (x).

4. GERAK HARMONIS SEDERHANA

Gerak harmonis sederhana yang dapat dijumpai dalam kehidupan sehari-hari adalah getaran benda pada pegas dan getaran benda pada ayunan sederhana. Kita akan mempelajarinya satu persatu.

Gerak Harmonis Sederhana pada Ayunan

Ketika beban digantungkan pada ayunan dan tidak diberikan gaya maka benda akan diam di titik kesetimbangan B. Jika beban ditarik ke titik A dan dilepaskan, maka beban akan bergerak ke B, C, lalu kembali lagi ke A. Gerakan beban akan terjadi berulang secara periodik, dengan kata lain beban pada ayunan di atas melakukan gerak harmonik sederhana

Simpangan, Kecepatan, dan Percepatan GHS

a. Simpangan GHS

1. 1. Untuk menghitung besarnya simpangan pada gerak harmonis sederhana digunakan rumus:
      

      atau Bila besarnya sudut awal (Θ ₀) adalah 0 maka persamaan simpangannya menjadi:
      dengan:
      y = simpangan (m)
      A = amplitudo atau simpangan maksimum (m)
      t = waktu getar (s)
      w = kecepatan sudut (rad/s)
      Simpangan akan bernilai maksimum (y_maks) jika sin wt = 1 sehingga persamaannya menjadi:
      
   2. Kecepatan GHS

      Besarnya kecepatan gerak harmonis dapat dicari dengan persamaan:
      

      Besarnya kecepatan akan mencapai nilai maksimun bila besarnya cos wt = 1, sehingga persamaannya menjadi:
      
   3. Percepatan GHS

      Besarnya percepatan pada gerak harmonis sederhana dapat dihitung dengan rumus:
      

      atau Dan besarnya percepatan akan mencapai nilai maksimal apabila besarnya sin wt = 1, sehingga:
      Besarnya percepatan bernilai negatif menunjukkan arah percepatan a berlawanan dengan arah perpindahan y (y adalah perpindahan dari titik keseimbangan)
   
   Sudut Fase, Fase, dan Beda Fase GHS
   

   Berdasarkan dari persamaan simpangan:
   

   
   bila diturunkan akan menjadi,
   Faktor Θ disebut sudut fase, yaitu posisi sudut selama benda bergerak harmonis.

   Fase atau tingkat getar adalah sudut fase dibagi dengan sudut tempuh selama satu putaran penuh. Sehingga besarnya fase dapat dihitung dari persamaan:
   

   Nilai fase biasanya hanya diambil bilangan pecahannya saja Misalkannya saja besarnya fase getaran adalah ¹/₄, 1¹/₄, 2¹/₄ maka besarnya fase cukup disebut ¹/₄ saja karena posisi partikel yang bergetar untuk ketiga fase getar tersebut sama. Bilangan bulat di depan pecahan, menunjukkan banyaknya getaran penuh yang terlewati.

   Pembahasan tentang fase dibagi menjadi dua, yaitu:

   1. Beda fase getaran suatu titik dengan selang waktu t= t₁ dan t= t₂
      Persamaan yang dipakai untuk menghitung besarnya beda fase dengan selang waktu dari t₁ sampai t₂ adalah:
      
   2. Beda fase dua getaran pada waktu sama
      Kita juga dapat menghitung beda fase dua getaran pada waktu yang sama. Misalkan dua getaran masing - masing dengan periode T₁ dan T₂ maka beda fase keduanya setelah bergetar selama t sekon dapat dicari dengan persamaan:
      
      Dua kedudukan tersebut akan dikatan sefase bila nilai beda fase merupakan bilangan cacah (tanpa pecahan ataupun desimal). Sebaliknya kedudukan akan dikatakan berlawanan fase apabila nilai beda fase berupa bilangan cacah+¹/₂(dengan pecahan ataupun desimal).
2. Superposisi Dua Simpangan Gerak Harmonis yang Segaris

   Jika ada dua persamaan simpangan yang dialami oleh suatu partikel pada saat yang sama, maka simpangan akibat kedua getaran dapat dicaari dengan dua cara, yaitu secara grafis dan secara maematis. Berikut adalah pembahasan mengenai kedua cara tersebut.

   1. Secara Grafis

      Berikut adalah gambar Superposisi dua gerak harmonis sederhana,
      

      
   2. Secara Matematis

      Dalam perhitungan secara matematis dua gerak harmonis memiliki simpangannya masing - masing. Untuk mencari simpangan superposisinya maka kedua simpangan itu dijumlahkan (y = y₁ + y₂) sehingga didapatkan persamaan sebagai berikut:
      

      
3. Penurunan Rumus Periode (T) dan Frekuensi (f)

   Dalam pembahasan suba bab ini, kita akan membahasa mengenai Periode (T) dan frekuensi (f). Dalam bahasan ini, akan membahas pula mengenai gaya pemulih. Karena itu, pembahasannya akan dibatasi hanya sampai pada pegas dan ayunan sederhana.

   1. Pegas

      Dalam pegas untuk perhitungan Periodenya digunakan rumus:
      

      sedangkan besarnya frekuensi berbanding terbalik dengan periodenya ( f = 1/T), sehingga didapatkan rumus frekuensi sebagai berikut:
      
      dengan,
      m = massa beban (kg)
      k = konstanta pegas (N/m)Sedangkan bila konstanta pegas belum diketahui, konstatanya dapat dihitung dengan persamaan:
      
      dengan,
      g = gaya gravitasi (9,8 N/kg atau 10 N/kg)
      x = perpanjangan pegas (m) Bila pegas yang dipakai lebih dari satu, maka untuk mencari konstantanya harus menggunakan konstanta total. Untuk menghitung konstanta total tergantung dari rangkaian pegas itu sendiri. Bila beberapa pegas dirangkai secara seri, maka untuk mencari konstanta totalnya mengunakan rumus:
      Sedangkan untuk pegas yang dirangkai paralel mengunakan rumus:
      
   2. Ayunan Sederhana

      Sedangkan dalam ayunan sederhana untuk mencari besarnya Periode digunakan rumus:
      

      Kemudian dalam mencari frekuensi, karena nilai frekuensi berbanding terbalik dengan periode maka didapatkan rumus:
      
      dengan,
      l = panjang tali (m)
      g = gaya gravitasi bumi (m/s²)

5. USAHA DAN ENERGI

a. USAHA

Usaha alias Kerja yang dilambangkan dengan huruf W , digambarkan sebagai sesuatu yang dihasilkan oleh Gaya (F) ketika Gaya bekerja pada benda hingga benda bergerak dalam jarak tertentu. Hal yang paling sederhana adalah apabila Gaya (F) bernilai konstan (baik besar maupun arahnya) dan benda yang dikenai Gaya bergerak pada lintasan lurus dan searah dengan arah Gaya tersebut.

Secara matematis, usaha yang dilakukan oleh gaya yang konstan didefinisikan sebagai hasil kali perpindahan dengan gaya yang searah dengan perpindahan.

Persamaan matematisnya adalah :

W = Fs cos 0 = Fs (1) = Fs

W adalah usaha alias kerja, F adalah besar gaya yang searah dengan perpindahan dan s adalah besar perpindahan.

Apabila gaya konstan tidak searah dengan perpindahan, sebagaimana tampak pada gambar di bawah, maka usaha yang dilakukan oleh gaya pada benda didefinisikan sebagai perkalian antara perpindahan dengan komponen gaya yang searah dengan perpindahan. Komponen gaya yang searah dengan perpindahan adalah F cos teta

Secara matematis dirumuskan sebagai berikut :

Hasil perkalian antara besar gaya (F) dan besar perpindahan (s) di atas merupakan bentuk perkalian titik atau perkalian skalar. Karenanya usaha masuk dalam kategori besaran skalar. Pelajari lagi perkalian vektor dan skalar kalau dirimu bingun… Persamaan di atas bisa ditulis dalam bentuk seperti ini :

Satuan Usaha dalam Sistem Internasional (SI) adalah newton-meter. Satuan newton-meter juga biasa disebut Joule ( 1 Joule = 1 N.m). menggunakan sistem CGS (Centimeter Gram Sekon), satuan usaha disebut erg. 1 erg = 1 dyne.cm. Dalam sistem British, usaha diukur dalam foot-pound (kaki-pon). 1 Joule = 10⁷ erg = 0,7376 ft.lb.

Perlu anda pahami dengan baik bahwa sebuah gaya melakukan usaha apabila benda yang dikenai gaya mengalami perpindahan. Jika benda tidak berpindah tempat maka gaya tidak melakukan usaha. Agar memudahkan pemahaman anda, bayangkanlah anda sedang menenteng buku sambil diam di tempat. Walaupun anda memberikan gaya pada buku tersebut, sebenarnya anda tidak melakukan usaha karena buku tidak melakukan perpindahan. Ketika anda menenteng atau menjinjing buku sambil berjalan lurus ke depan, ke belakang atau ke samping, anda juga tidak melakukan usaha pada buku. Pada saat menenteng buku atau menjinjing tas, arah gaya yang diberikan ke atas, tegak lurus dengan arah perpindahan. Karena tegak lurus maka sudut yang dibentuk adalah 90^o. Cos 90^o = 0, karenanya berdasarkan persamaan di atas, nilai usaha sama dengan nol. Contoh lain adalah ketika dirimu mendorong tembok sampai puyeng… jika tembok tidak berpindah tempat maka walaupun anda mendorong sampai banjir keringat, anda tidak melakukan usaha. Kita dapat menyimpulkan bahwa sebuah gaya tidak melakukan usaha apabila gaya tidak menghasilkan perpindahan dan arah gaya tegak lurus dengan arah perpindahan.

b. ENERGI

Segala sesuatu yang kita lakukan dalam kehidupan sehari-hari membutuhkan energi. Untuk bertahan hidup kita membutuhkan energi yang diperoleh dari makanan. Setiap kendaraan membutuhkan energi untuk bergerak dan energi itu diperoleh dari bahan bakar. Hewan juga membutuhkan energi untuk hidup, sebagaimana manusia dan tumbuhan.

Energi merupakan salah satu konsep yang paling penting dalam fisika. Konsep yang sangat erat kaitannya dengan usaha adalah konsep energi. Secara sederhana, energi merupakan kemampuan melakukan usaha. Definisi yang sederhana ini sebenarnya kurang tepat atau kurang valid untuk beberapa jenis energi (misalnya energi panas atau energi cahaya tidak dapat melakukan kerja). Definisi tersebut hanya bersifat umum. Secara umum, tanpa energi kita tidak dapat melakukan kerja. Sebagai contoh, jika kita mendorong sepeda motor yang mogok, usaha alias kerja yang kita lakukan menggerakan sepeda motor tersebut. Pada saat yang sama, energi kimia dalam tubuh kita menjadi berkurang, karena sebagian energi kimia dalam tubuh berubah menjadi energi kinetik
sepeda motor. Usaha dilakukan ketika energi dipindahkan dari satu benda ke benda lain. Contoh ini juga menjelaskan salah satu konsep penting dalam sains, yakni kekekalan energi. Jumlah total energi pada sistem dan lingkungan bersifat kekal alias tetap. Energi tidak pernah hilang, tetapi hanya dapat berubah bentuk dari satu bentuk energi menjadi bentuk energi lain. Mengenai Hukum Kekekalan Energi akan kita kupas tuntas dalam pokok bahasan tersendiri.
6. MOMENTUM, IMPULS, DAN TUMBUKAN

Definisi Momentum

Momentum adalah sebuah nilai dari perkalian materi yang bermassa / memiliki bobot dengan pergerakan / kecepatan. Dalam Fisika momentum dilambangkan dengan huruf ‘p’, secara matematis momentum dapat dirumuskan :

p= m . v
p = momentum, m = massa, v = kecepatan / viscositas (dalam fluida)

Momentum akan berubah seiring dengan perubahan massa dan kecepatan. Semakin cepat pergerakan suatu materi/benda akan semakin besar juga momentumnya. Semakin besar momentum, maka semakin dahsyat kekuatan yang dimiliki oleh suatu benda. Jika materi dalam keadaan diam, maka momentumnya sama dengan nol. Sebaliknya semakin cepat pergerakannya, semakin besar juga momentumnya. (Filosofi : Jika manusia tidak mau bergerak / malas, maka hasil kerjanya sama dengan nol).

Definisi Impuls

Impuls adalah selisih dari momentum atau momentum awal dikurangi momentum akhir. Dalam Fisika impuls dilambangkan dengan simbol / huruf "I". Secara matematis impuls dirumuskan :

I = p2 – p1 = ∆p
I = m.v2 – m.v1
I = m(v2 – v1)
I = m. ∆v

Karena m = F/a (bisa dibaca di Aplikasi Hukum Newton Dalam Kehidupan) , maka :

I = F/a . ∆v
I = [F/(∆v/∆t)] . ∆v
I = F . ∆t
F = I/∆t

I = impuls, p1 = momentum awal, p2 = momentum akhir, F = gaya, ∆t = waktu sentuh, ∆v = selisih kecepatan

Nah, dari rumus F = I/∆t inilah letak pemanfaatan aplikasi momentum dan impuls. Semakin kecil waktu sentuh, maka semakin besar gaya yang akan diterima benda. Semakin lama waktu sentuh, maka semakin kecil gaya yang diterima benda.

Aplikasi Momentum dan Impuls

Mobil di desain untuk mudah penyok, hal ini bertujuan untuk memperbesar waktu sentuh untuk memperkecil gaya yang diterima oleh pengendara. Dengan demikian diharapkan, keselamatan pengemudi lebih dapat terjamin. Jika kecepatannya besar, maka gaya yang diterima akan besar, sehingga pengendara akan mengalami kecelakaan yang fatal. Jadi pesan saya jangan ngebut, walaupun mobil sudah di design sedemikian rupa.

Balon udara pada mobil juga bertujuan untuk memperlambat waktu sentuh antara kepala pengemudi dengan setir mobil. Ingat, semakin besar waktu sentuh, maka semakin kecil gaya yang akan mengenai kepala pengemudi. Sabuk pengaman juga fungsi dan cara kerjanya sama dengan balon udara pada mobil, yakni untuk mengurangi waktu sentuh antara pengemudi dengan dashboard mobil pada saat bersentuhan.

JENIS-JENIS TUMBUKAN

Perlu anda ketahui bahwa biasanya dua benda yang bertumbukan bergerak mendekat satu dengan yang lain dan setelah bertumbukan keduanya bergerak saling menjauhi. Ketika benda bergerak, maka tentu saja benda memiliki kecepatan. Karena benda tersebut mempunyai kecepatan (dan massa), maka benda itu pasti memiliki momentum (p = mv) dan juga Energi Kinetik (EK = ½ mv²).

TUMBUKAN LENTING SEMPURNA

Tumbukan lenting sempurna tu maksudnya bagaimanakah ? Dua benda dikatakan melakukan Tumbukan lenting sempurna jika Momentum dan Energi Kinetik kedua benda sebelum tumbukan = momentum dan energi kinetik setelah tumbukan. Dengan kata lain, pada tumbukan lenting sempurna berlaku Hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik.

Sekarang mari kita tinjau persamaan Hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik pada perisitiwa Tumbukan Lenting Sempurna. Untuk memudahkan pemahaman dirimu, perhatikan gambar di bawah.

Dua benda, benda 1 dan benda 2 bergerak saling mendekat. Benda 1 bergerak dengan kecepatan v₁ dan benda 2 bergerak dengan kecepatan v₂. Kedua benda itu bertumbukan dan terpantul dalam arah yang berlawanan. Perhatikan bahwa kecepatan merupakan besaran vektor sehingga dipengaruhi juga oleh arah. Sesuai dengan kesepakatan, arah ke kanan bertanda positif dan arah ke kiri bertanda negatif. Karena memiliki massa dan kecepatan, maka kedua benda memiliki momentum (p = mv) dan energi kinetik (EK = ½ mv²). Total Momentum dan Energi Kinetik kedua benda sama, baik sebelum tumbukan maupun setelah tumbukan.

Secara matematis, Hukum Kekekalan Momentum dirumuskan sebagai berikut :

Keterangan :

m₁ = massa benda 1, m₂ = massa benda 2

v₁ = kecepatan benda sebelum tumbukan dan v₂ = kecepatan benda 2 Sebelum tumbukan

v’₁ = kecepatan benda Setelah tumbukan, v’₂ = kecepatan benda 2 setelah tumbukan

Jika dinyatakan dalam momentum,

m₁v₁ = momentum benda 1 sebelum tumbukan, m₁v’₁ = momentum benda 1 setelah tumbukan

m₂v₂ = momentum benda 2 sebelum tumbukan, m₂v’₂ = momentum benda 2 setelah tumbukan

Pada Tumbukan Lenting Sempurna berlaku juga Hukum Kekekalan Energi Kinetik. Secara matematis dirumuskan sebagai berikut :

TUMBUKAN LENTING SEBAGIAN

Pada tumbukan lenting sebagian, Hukum Kekekalan Energi Kinetik tidak berlaku karena ada perubahan energi kinetik terjadi ketika pada saat tumbukan. Perubahan energi kinetik bisa berarti terjadi pengurangan Energi Kinetik atau penambahan energi kinetik. Pengurangan energi kinetik terjadi ketika sebagian energi kinetik awal diubah menjadi energi lain, seperti energi panas, energi bunyi dan energi potensial. Hal ini yang membuat total energi kinetik akhir lebih kecil dari total energi kinetik awal. Kebanyakan tumbukan yang kita temui dalam kehidupan sehari-hari termasuk dalam jenis ini, di mana total energi kinetik akhir lebih kecil dari total energi kinetik awal. Tumbukan antara kelereng, tabrakan antara dua kendaraan, bola yang dipantulkan ke lantai dan lenting ke udara, dll.

Sebaliknya, energi kinetik akhir total juga bisa bertambah setelah terjadi tumbukan. Hal ini terjadi ketika energi potensial (misalnya energi kimia atau nuklir) dilepaskan. Contoh untuk kasus ini adalah peristiwa ledakan.

Suatu tumbukan lenting sebagian biasanya memiliki koofisien elastisitas (e) berkisar antara 0 sampai 1. Secara matematis dapat ditulis sebagai berikut :

Bagaimana dengan Hukum Kekekalan Momentum ? Hukum Kekekalan Momentum tetap berlaku pada peristiwa tumbukan lenting sebagian, dengan anggapan bahwa tidak ada gaya luar yang bekerja pada benda-benda yang bertumbukan.

TUMBUKAN TIDAK LENTING SAMA SEKALI

Bagaimana dengan tumbukan tidak lenting sama sekali ? suatu tumbukan dikatakan Tumbukan Tidak Lenting sama sekali apabila dua benda yang bertumbukan bersatu alias saling menempel setelah tumbukan. Salah satu contoh populer dari tumbukan tidak lenting sama sekali adalah pendulum balistik. Pendulum balistik merupakan sebuah alat yang sering digunakan untuk mengukur laju proyektil, seperti peluru. Sebuah balok besar yang terbuat dari kayu atau bahan lainnya digantung seperti pendulum. Setelah itu, sebutir peluru ditembakkan pada balok tersebut dan biasanya peluru tertanam dalam balok. Sebagai akibat dari tumbukan tersebut, peluru dan balok bersama-sama terayun ke atas sampai ketinggian tertentu (ketinggian maksimum). Lihat gambar di bawah…

Apakah pada Tumbukan Tidak Lenting Sama sekali berlaku hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik ?

Perhatikan gambar di atas. Hukum kekekalan momentum hanya berlaku pada waktu yang sangat singkat ketika peluru dan balok bertumbukan, karena pada saat itu belum ada gaya luar yang bekerja. Secara matematis dirumuskan sebagai berikut :

m₁v₁ + m₂v₂ = m₁v’₁ + m₂v’₂

m₁v₁ + m₂(0) = (m₁ + m₂) v’

m₁v₁ = (m₁ + m₂) v’—- persamaan 1