Hukum kekekalan momentum diterapkan pada proses tumbukan semua jenis, dimana prinsip impuls mendasari proses tumbukan dua benda, yaitu I1 = -I2.
Jika dua benda A dan B dengan massa masing-masing MA dan MB serta kecepatannya masing-masing VA dan VB saling bertumbukan, maka :
MA VA + MB VB = MA VA + MB VB
VA dan VB = kecepatan benda A dan B pada saat tumbukan
VA dan VB = kecepatan benda A den B setelah tumbukan.
Dalam penyelesaian soal, searah vektor ke kanan dianggap positif, sedangkan ke kiri dianggap negatif.
Dua benda yang bertumbukan akan memenuhi tiga keadaan/sifat ditinjau dari keelastisannya,
a. ELASTIS SEMPURNA : e = 1
e = (- VA' - VB')/(VA - VB)
e = koefisien restitusi.
Disini berlaku hukum kokokalan energi den kokekalan momentum.
b. ELASTIS SEBAGIAN: 0 <>Disini hanya berlaku hukum kekekalan momentum.
Khusus untuk benda yang jatuh ke tanah den memantul ke atas lagi maka koefisien restitusinya adalah:
e = h'/h
h = tinggi benda mula-mula
h' = tinggi pantulan benda
C. TIDAK ELASTIS: e = 0
Setelah tumbukan, benda melakukan gerak yang sama dengan satu kecepatan v',
MA VA + MB VB = (MA + MB) v'
Disini hanya berlaku hukum kekekalan momentum
Pada awal perkembangan roket, roket digerakan dari hasil pembakaran bahan bakar minyak gas dan oksigen cair, untuk menghasilkan gas panas yang meledak ke bawah dan mendorong roket ke atas. Untuk roket V-2 yang dikembangkan Hitler, menggunakan turbin uap untuk memompa alkohol dan oksigen cair ke dalam ruang bakar yang menghasilkan ledakan beruntun yang mendorong roket ke atas. Prinsip kerja roket merupakan penerapan dari Hukum Newton III tentang gerak, dimana energi panas diubah menjadi energi gerak.
Prinsip kerja dari roket berbahan bakar cair dan padat sama, di mana hasil pembakaran menghasilkan gaya dorong ke atas. Kelebihan dari roket berbahan bakar padat mampu menyimpan bahan bakar dengan dengan jumlah besar untuk ruang penyimpanan yang sama, karena telah dipadatkan, sedangkan bahan bakar cair tidak bisa dimampatkan.
DINAMIKA ROTASI

MOMEN GAYA ( t ) adalah gaya kali jarak/lengan.
Arah gaya dan arah jarak harus tegak lurus.
Untuk benda panjang:
| Untuk benda berjari jari:
|
F = gaya penyebab benda berotasi
R = jari-jari
I = lengan gaya terhadap sumbu
I = m . R2 = momen inersia benda
a = percepatan sudut / angular
MOMEN INERSIA
Momen inersia (satuan SI kg m2) adalah ukuran ketahanan objek terhadap perubahan laju Besaran ini adalah analog rotasi daripada rotasinya massa. Dengan kata lain, besaran ini adalah kelembaman sebuah benda tegar yang berputar terhadap rotasinya. Momen inersia berperan dalam dinamika rotasi seperti massa dalam dinamika dasar, dan menentukan hubungan antara momentum sudut dan kecepetan sudut, momen gaya dan percepatan sudut, dan beberapa besaran lain. Meskipun pembahasan skalar terhadap momen inersia, pembahasan menggunakan pendekatan tensor memungkinkan analisis sistem yang lebih rumit seperti gerakan giroskopik.
Lambang I dan kadang-kadang juga J biasanya digunakan untuk merujuk kepada momen inersia.
Definisi skalar
Definisi sederhana momen inersia (terhadap sumbu rotasi tertentu) dari sembarang objek, baik massa titik atau struktur tiga dimensi, diberikan oleh rumus:
di mana m adalah massa dan r adalah jarak tegak lurus terhadap sumbu rotasi.
Analisis
Momen inersia (skalar) sebuah massa titik yang berputar pada sumbu yang diketahui didefinisikan oleh
Momen inersia adalah aditif. Jadi, untuk sebuah bend tegar yang terdiri atas N massa titik mi dengan jarak ri terhadap sumbu rotasi, momen inersia total sama dengan jumlah momen inersia semua massa titik:
Untuk benda pejal yang dideskripsikan oleh fungsi kerapatan massa ρ(r), momen inersia terhadap sumbu tertentu dapat dihitung dengan mengintegralkan kuadrat jarak terhadap sumbu rotasi, dikalikan dengan kerapatan massa pada suatu titik di benda tersebut:
di mana
- V adalah volume yang ditempati objek
- ρ adalah fungsi kerapatan spasial objek
- r = (r,θ,φ), (x,y,z), atau (r,θ,z) adalah vektor (tegaklurus terhadap sumbu rotasi) antara sumbu rotasi dan titik di benda tersebut.
Berdasarkan analisis dimensi saja, momen inersia sebuah objek bukan titik haruslah mengambil bentuk:
di mana
- M adalah massa
- R adalah jari-jari objek dari pusat massa (dalam beberapa kasus, panjang objek yang digunakan)
- k adalah konstanta tidak berdimensi yang dinamakan "konstanta inersia", yang berbeda-beda tergantung pada objek terkait.
Konstanta inersia digunakan untuk memperhitungkan perbedaan letak massa dari pusat rotasi. Contoh:
- k = 1, cincin tipis atau silinder tipis di sekeliling pusat
- k = 2/5, bola pejal di sekitar pusat
- k = 1/2, silinder atau piringan pejal di sekitar pusat.
Momen Gaya (Torsi = τ)
 karena aт = r α, maka
karena aт = r α, makaTitik Pusat Massa dan Titik (Pusat) Berat
Jenis Keseimbangan
|
| |
|
|  |
|
| |
|
|  |
Fluida ( zat alir ) adalah zat yang dapat mengalir, misalnya zat cair dan gas. Fluida dapat digolongkan dalam dua macam, yaitu fluida statis dan dinamis.
TEKANAN HIDROSTATIS
Tekanan hidrostatis ( Ph) adalah tekanan yang dilakukan zat cair pada bidang dasar tempatnya.
PARADOKS HIDROSTATIS
Gaya yang bekerja pada dasar sebuah bejana tidak tergantung pada bentuk bejana dan jumlah zat cair dalam bejana, tetapi tergantung pada luas dasar bejana ( A ), tinggi ( h ) dan massa jenis zat cair ( r )
dalam bejana.
| Ph = r g h
Pt = Po + Ph F = P h A = r g V | r = massa jenis zat cair
h = tinggi zat cair dari permukaan g = percepatan gravitasi Pt = tekanan total Po = tekanan udara luar |  |
HUKUM PASCAL
Tekanan yang dilakukan pada zat cair akan diteruskan ke semua arah sama.
P1 = P2 ® F1/A1 = F2/A2
HUKUM ARCHIMEDES
Benda di dalam zat cair akan mengalami pengurangan berat sebesar berat zat cair yang dipindahkan.
Tiga keadaan benda di dalam zat cair:
| a. tenggelam: W>Fa Þ rb > rz
b. melayang: W = Fa Þ rb = rz c. terapung: W=Fa Þ rb.V=rz.V' ; rb<rz |  |
W = berat benda
Fa = gaya ke atas = rz . V' . g
rb = massa jenis benda
rz = massa jenis fluida
V = volume benda
V' = volume benda yang berada dalam fluida
Akibat adanya gaya ke atas ( Fa ), berat benda di dalam zat cair (Wz) akan berkurang menjadi:
Wz = W - Fa
Wz = berat benda di dalam zat cair
TEGANGAN PERMUKAAN
Tegangan permukaan ( g) adalah besar gaya ( F ) yang dialami pada permukaan zat cair persatuan panjang(l)
g = F / 2l
KAPILARITAS
Kapilaritas ialah gejala naik atau turunnya zat cair ( y ) dalam tabung kapiler yang dimasukkan sebagian ke dalam zat cair karena pengarah adhesi dan kohesi.
 |  |
y = 2 g cos q / r g r
y = kenaikan/penurunan zat cair pada pipa (m)
g = tegangan permukaan (N/m)
q = sudut kontak (derajat)
p = massa jenis zat cair (kg / m3)
g = percepatan gravitas (m / det2)
r = jari-jari tabung kapiler (m)
FLUIDA DINAMIS
Sifat Fluida Ideal:
- tidak dapat ditekan (volume tetap karena tekanan)
- dapat berpindah tanpa mengalami gesekan
- mempunyai aliran stasioner (garis alirnya tetap bagi setiap partikel)
- kecepatan partikel-partikelnya sama pada penampang yang sama
HUKUM BERNOULLI
Hukum ini diterapkan pada zat cair yang mengalir dengan kecepatan berbeda dalam suatu pipa.
| P + r g Y + 1/2 r v2 = c P = tekanan
|
]® tiap satuan
|  |
CEPAT ALIRAN (DEBIT AIR)
Cepat aliran (Q) adalah volume fluida yang dipindahkan tiap satuan waktu.
Q = A . v
A1 . v1 = A2 . v2
v = kecepatan fluida (m/det)
A = luas penampang yang dilalui fluida
Untuk zat cair yang mengalir melalui sebuah lubang pada tangki, maka besar kecepatannya selalu dapat diturunkan dari Hukum Bernoulli, yaitu:
| v = Ö(2gh) | h = kedalaman lubang dari permukaan zat cair |
Contoh:
1. Sebuah kolam air berdinding bujursangkar dengan panjang 15 m, tingginya 7,5m.Tentukanlah tekanan air 4,5 m di bawah permukaan air!
Jawab:
P = r . g . h = 103 . 10 . 4,5
P = 4,5.104 N/m2
2. Air mengalir sepanjang pipa horisontal, penampang tidak sama besar. Pada tempat dengan kecepatan air 35 cm/det tekanannya adalah 1 cmHg. Tentukanlah tekanan pada bagian pipa dimana kecepatan aliran airnya 65 cm/det.(g = 980 cm/det2) !
Jawab:
P1 = 1 cmHg = 1.13,6.980 dyne/cm2
P1 = 13328 dyne/cm2
v1 = 35 cm/det; v2 = 65 cm/det

Prinsip Bernoulli:
P1 + pgy1 + 1/2rv12 = P2 + rgy2 + 1/2rv22
Karena y1 = y2 (pipa horisontal), maka:
P1 - P2 = 1/2 r (V22 - V12)
P1 - P2 = 1/2 1 (652 352)
P1 - P2 = 1/2 3000
P1 - P2 = 1500 dyne/cm2
Jadi:
P2 = P1 - 1500
P2 = 13328 - 1500
P2 = 11828 dyne/cm
P2 = 0,87 cmHg
HUKUM ARCHIMIDES
Apabila benda yang dimasukkan ke dalam fluida, terapung, di mana bagian benda yang tercelup hanya sebagian maka volume fluida yang dipindahkan = volume bagian benda yang tercelup dalam fluida tersebut. Tidak peduli apapun benda dan bagaimana bentuk benda tersebut, semuanya akan mengalami hal yang sama. Ini adalah buah karya eyang butut Archimedes (287-212 SM) yang saat ini diwariskan kepada kita dan lebih dikenal dengan julukan “Prinsip Archimedes”. Prinsip Archimedes menyatakan bahwa :
Ketika sebuah benda tercelup seluruhnya atau sebagian di dalam zat cair, zat cair akan memberikan gaya ke atas (gaya apung) pada benda, di mana besarnya gaya ke atas (gaya apung) sama dengan berat zat cair yang dipindahkan.
PERSAMAAN TEGANGAN PERMUKAAN
Jika kawat U dimasukan ke dalam larutan sabun, maka setelah dikeluarkan akan terbentuk lapisan air sabun pada permukaan kawat tersebut. Mirip seperti ketika dirimu bermain gelembung sabun. Karena kawat lurus bisa digerakkan dan massanya tidak terlalu besar, maka lapisan air sabun akan memberikan gaya tegangan permukaan pada kawat lurus sehingga kawat lurus bergerak ke atas (perhatikan arah panah). Untuk mempertahankan kawat lurus tidak bergerak (kawat berada dalam kesetimbangan), maka diperlukan gaya total yang arahnya ke bawah, di mana besarnya gaya total adalah F = w + T. Dalam kesetimbangan, F = gaya tegangan permukaan yang dikerjakan oleh lapisan air sabun pada kawat lurus.
Misalkan panjang kawat lurus adalah l. Karena lapisan air sabun yang menyentuh kawat lurus memiliki dua permukaan, maka gaya tegangan permukaan yang ditimbulkan oleh lapisan air sabun bekerja. Tegangan permukaan pada lapisan sabun merupakan perbandingan antara Gaya Tegangan Permukaan (F) dengan panjang permukaan di mana gaya bekerja (d). Untuk kasus ini, panjang permukaan adalah 2l.
Karena tegangan permukaan merupakan perbandingan antara Gaya tegangan permukaan dengan Satuan panjang, maka satuan tegangan permukaan adalah Newton per meter (N/m) atau dyne per centimeter (dyn/cm).
1 dyn/cm = 10-3 N/m = 1 mN/m
TERMODINAMIKA
Termodinamika (bahasa Yunani: thermos = 'panas' and dynamic = 'perubahan') adalah fisika energi , panas, kerja, entropi dan kespontanan proses. Termodinamika berhubungan dekat dengan mekanika statistik di mana banyak hubungan termodinamika berasal.
Hukum kekekalan energi adalah salah satu dari hukum-hukum kekekalan yang meliputi energi kinetik dan energi potensial. Hukum ini adalah hukum pertama dalam termodinamika.
Asas Black adalah suatu prinsip dalam termodinamika yang dikemukakan oleh Joseph Black. Asas ini menjabarkan:
* Jika dua buah benda yang berbeda yang suhunya dicampurkan, benda yang panas memberi kalor pada benda yang dingin sehingga suhu akhirnya sama
* Jumlah kalor yang diserap benda dingin sama dengan jumlah kalor yang dilepas benda panas
* Benda yang didinginkan melepas kalor yang sama besar dengan kalor yang diserap bila dipanaskan
Rumus Asas Black =
(M1 X C1) (T1-Ta) = (M2 X C2) (Ta-T2)
Catatan :
M1 = Massa benda yang mempunyai tingkat temperatur lebih tinggi
C1 = Kalor jenis benda yang mempunyai tingkat temperatur lebih tinggi
Ta = Temperatur benda yang mempunyai tingkat temperatur lebih tinggi
T1 = Temperatur akhir pencampuran kedua benda
M2 = Massa benda yang mempunyai tingkat temperatur lebih rendah
C2 = Kalor jenis benda yang mempunyai tingkat temperatur lebih rendah
T2 = Temperatur benda yang mempunyai tingkat temperatur lebih rendah
HUKUM I TERMODINAMIKA
Hukum Kekekalan Energi (Hukum I Termodinamika) berbunyi: "Energi dapat berubah dari satu bentuk ke bentuk yang lain tapi tidak bisa diciptakan ataupun dimusnahkan (konversi energi)".
Keterangan :
delta U = Perubahan energi dalam
Q = Kalor
W = Kerja
Hukum pertama termodinamika merupakan pernyataan Hukum Kekekalan Energi dan ketepatannya telah dibuktikan melalui banyak percobaan (seperti percobaan om Jimi Joule). Perlu diketahui bahwa hukum ini dirumuskan pada abad kesembilan belas, setelah kalor dipahami sebagai energi yang berpindah akibat adanya perbedaan suhu.
HUKUM II TERMODINAMIKA
Kalor berpindah dengan sendirinya dari benda bersuhu tinggi ke benda bersuhu rendah; kalor tidak akan berpindah dengan sendirinya dari benda bersuhu rendah ke benda bersuhu tinggi (Hukum kedua termodinamika




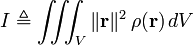

 adalah jari-jari yang digunakan untuk menentukan momen inersia
adalah jari-jari yang digunakan untuk menentukan momen inersia